Alternated hypercubic honeycomb


An alternated square tiling is another square tiling, but having two types of squares, alternating in a checkerboard pattern.
A twice alternated square tiling.

A partially-filled alternated cubic honeycomb with tetrahedral and octahedral cells.
A subsymmetry colored alternated cubic honeycomb.

In geometry, the alternated hypercube honeycomb (or demicubic honeycomb) is a dimensional infinite series of honeycombs, based on the hypercube honeycomb with an alternation operation. It is given a Schläfli symbol h{4,3...3,4} representing the regular form with half the vertices removed and containing the symmetry of Coxeter group 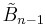{\tilde{B}}_{n-1} for n ≥ 4. A lower symmetry form {\tilde{D}}_{n-1} can be created by removing another mirror on a order-4 peak.

The alternated hypercube facets become demihypercubes, and the deleted vertices create new orthoplex facets. The vertex figure for honeycombs of this family are rectified orthoplexes.

These are also named as hδn for an (n-1)-dimensional honeycomb.

hδn Name Schläfli
symbol		 Coxeter-Dynkin diagrams
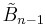{\tilde{B}}_{n-1} {\tilde{D}}_{n-1}
hδ2 Apeirogon {∞}
 
hδ3 Alternated square tiling
(Same as regular square tiling {4,4})		 h{4,4}=t1{4,4}
t0,2{4,4}
hδ4 Alternated cubic honeycomb h{4,3,4}
{31,1,4}
hδ5 Alternated tesseractic honeycomb or
demitesseractic tetracomb
(Same as regular {3,3,4,3})		 h{4,32,4}
{31,1,3,4}
{31,1,1,1}
hδ6 Demipenteractic honeycomb h{4,33,4}
{31,1,32,4}
{31,1,3,31,1}
hδ7 Demihexeractic honeycomb h{4,34,4}
{31,1,33,4}
{31,1,32,31,1}
hδ8 Demihepteractic honeycomb h{4,35,4}
{31,1,34,4}
{31,1,33,31,1}
hδ9 Demiocteractic honeycomb h{4,36,4}
{31,1,35,4}
{31,1,34,31,1}
hδ10 Demienneractic honeycomb h{4,37,4}
{31,1,36,4}
{31,1,35,31,1}
hδ11 Demidekeractic honeycomb h{4,38,4}
{31,1,37,4}
{31,1,36,31,1}
 
hδn n-demicubic honeycomb h{4,3n-3,4}
{31,1,3n-4,4}
{31,1,3n-5,31,1}		 ...

References